Python 코딩테스트 71~80

파이썬 코딩테스트 준비를 하며 공부한 내용을 기록하고 복습합니다.

참고자료

• coderbyte

파이썬 코딩테스트

문제 71

Tree Constructor

정수 쌍의 배열이 이진트리를 형성할 수 있는지 여부를 판단
정수 쌍 데이터: (‘자식노드’,’부모노드’)

• Input: [“(1,2)”, “(2,4)”, “(7,2)”]
  • Output: “true”
• Input: [“(1,2)”, “(2,4)”, “(5,7)”, “(7,2)”, “(9,5)”]
  • Output: true
• Input: [“(1,2)”, “(3,2)”, “(2,12)”, “(5,2)”]
  • Output: false

내가 제출한 코드

def TreeConstructor(strArr):
  edges = [ eval(x) for x in strArr ]
  nodes = set([ x for pair in edges for x in pair ])

  children = {}
  parents = {}
  for k,v in edges:
    p_set = parents.setdefault(k, set())
    p_set.add(v)
    c_set = children.setdefault(v, set())
    c_set.add(k)

  # binary tree
  # cond1: node must have 1 parent
  # cond2: node must have 2 child nodes
  cond1 = [ (k,len(v)) for k,v in parents.items() if len(v) > 1 ]
  cond2 = [ (k,len(v)) for k,v in children.items() if len(v) > 2 ]

  # print(cond1, cond2, '=>', not cond1 and not cond2)
  return "true" if not cond1 and not cond2 else "false"

# keep this function call here
print(TreeConstructor(input()))

문제 72

Shortest Path

첫번째 노드로부터 마지막 노드까지의 최단경로 찾기
(최단 경로가 없는 경우 ‘-1’ 반환)

• Input: [“4”,”A”,”B”,”C”,”D”,”A-B”,”B-D”,”B-C”,”C-D”]
  • 첫번째는 노드 개수, 이후 N개 노드 나열, 이후 간선 나열
  • Output: A-B-D
• Input: [“7”,”A”,”B”,”C”,”D”,”E”,”F”,”G”,”A-B”,”A-E”,”B-C”,”C-D”,”D-F”,”E-D”,”F-G”]
  • Output: A-E-D-F-G

내가 작성한 코드

재귀함수 짜는데 오래 걸림 (패턴을 외워두자)

# 재귀함수로 BFS 탐색
# - 브랜치마다 visited 새로 생성해야 함
# - paths 를 들고 다녀야 함 (모든 경로의 합산)
def find_paths(graph, end_node, curr, visited, paths):
  # found
  if curr == end_node:
    paths.append( visited )
    return
  # no edge (안하면 채점시 2점 감점)
  if curr not in graph:
    return
  # evaluate all branches
  for v in graph[curr]:
    if v not in visited:
      # with new list for visited
      find_paths(graph, end_node, v, visited+[v], paths)


def ShortestPath(strArr):
  # input
  N = int(strArr[0])
  nodes = strArr[1:N+1]
  start_node = nodes[0]
  end_node = nodes[-1]

  graph = {}
  for v1,v2 in [ tuple(e.split('-')) for e in strArr[N+1:] ]:
    # bidirectional
    temp = graph.setdefault(v1,set())
    temp.add(v2)
    temp = graph.setdefault(v2,set())
    temp.add(v1)
  # exception
  if not graph: return '-1'

  # find path
  paths = []
  visited = [start_node]
  find_paths(graph, end_node, start_node, visited, paths)

  # if not found
  if not paths:
    return '-1'

  # min, max 함수도 key 옵션이 있다
  s_path = min(paths, key=len)
  return '-'.join(s_path)

# keep this function call here
print(ShortestPath(input()))

다른 사람의 코드

반복방식은 탐색을 위해 모든 위치에서 이전 히스토리(경로)를 상태값으로 유지한다.

def ShortestPath(strArr):
  # input
  n = int(strArr[0])
  vertex = strArr[1:n+1]
  edges = strArr[n+1:]
  graph = {}
  for node in vertex:
    graph[node] = set()
  for e in edges:
    n1,n2 = e.split('-')
    graph[n1].add(n2)
    graph[n2].add(n1)

  # 반복방식 DFS : stack=[ (curr, visited) ]
  def dfs(graph, start, goal):
      # 발견된 모든 경로
      res = []
      # 상태값: 현재 위치와 visited 리스트
      stack = [ (start, [start]) ]
      while stack:
        (vertex, path) = stack.pop()
        if vertex in graph:
          # 방문하지 않은 인접 노드로
          for entry in (graph[vertex]-set(path)):
            # 발견시 경로 저장
            if entry == goal:
              res.append("-".join(path + [entry]))
            # 아니면, 새로운 visited 를 가지고 경로 탐색
            else:
              stack.append((entry, path + [entry]))
      return res

  # 모든 경로 중 최단 경로 반환
  ans = dfs(graph, vertex[0], vertex[-1])
  return -1 if ans == [] else sorted(ans, key = len)[0]

print(ShortestPath(input()))

문제 73

Weighted Path

최단 가중 경로 찾기

• Input: [“4”,”A”,”B”,”C”,”D”,”A

  B

  1”,”B

  D

  9”,”B

  C

  3”,”C

  D

  4”]

  • Output: A-B-C-D
• Input: [“7”,”A”,”B”,”C”,”D”,”E”,”F”,”G”,
  “A|B|1”,”A|E|9”,”B|C|2”,”C|D|1”,”D|F|2”,”E|D|6”,”F|G|2”]
  • Output: A-B-C-D-F-G

내가 제출한 코드

유사 문제라 금방 작성한다. (역시 다양한 문제를 풀어봐야)

def WeightedPath(strArr):
  # input
  N = int(strArr[0])
  nodes = strArr[1:N+1]
  start_node = nodes[0]
  end_node = nodes[-1]

  graph = {}
  for v1,v2,w in [ tuple(e.split('|')) for e in strArr[N+1:] ]:
    # bidirectional
    temp = graph.setdefault(v1,set())
    temp.add( (v2, int(w)) )
    temp = graph.setdefault(v2,set())
    temp.add( (v1, int(w)) )
  # exception
  if not graph: return '-1'

  def dfs_with_weight(goal, curr, paths):
    stack = [ (curr, [curr], 0) ]
    while stack:
      curr, visited, weight = stack.pop()
      # found
      if curr == goal:
        paths.append( (weight, visited) )
        continue

      # no edge (안하면 채점시 2점 감점)
      if curr not in graph:
          continue
      # branches
      for adj, wgt in graph[curr]:
        if adj not in visited:
          # with new visited and increased weight
          stack.append( (adj, visited+[adj], weight+wgt) )

  # find all paths with weight sum
  paths = []
  dfs_with_weight( end_node, start_node, paths )

  # 예외 처리
  if not paths: return '-1'

  path = min(paths, key=lambda p: (p[0],len(p[1])))
  return '-'.join(path[1])

# keep this function call here
print(WeightedPath(input()))

문제 74

Switch Sort

배열의 첫번째 요소를 최소값과 swap 하는 과정을 반복하며 정렬하기
정렬을 완료하기까지 필요한 swap 횟수 구하기

• Input: [3,1,2]
  • Output: 2
• Input: [1,3,4,2]
  • Output: 2

다른 사람의 코드

# 재귀함수
def SwitchSort(arr):
  # 종료 조건
  n = len(arr)
  steps = 0
  if n == 2:
    if arr[0] < arr[1]:
      return steps
    else:
      return steps + 1

  # 최소값 위치 찾기
  min_index = arr.index(min(arr))
  # 정렬된 상태면 다음 위치 정렬
  if min_index == 0:
    steps += SwitchSort(arr[1:])
  # 정렬되지 않았으면 arr[0]를 최소값 위치와 swap
  # 이후 다음 위치 정렬
  else:
    tmp = arr[0]
    arr[0] = arr[min_index]
    arr[min_index] = tmp
    steps += SwitchSort(arr[1:]) + 1
  # swap 횟수 반환
  return steps

# keep this function call here
print(SwitchSort(input()))

문제 75

Matrix Determinant

N x N 정방 행렬의 행렬식(determinant) 계산 (정방행렬이 아니면 -1 반환)
ex) 2 x 2 의 행렬([a,b,c,d])의 행렬식은 detA = ad-bc 이다.

• Input: [“1”,”2”,”<>”,”3”,”4”]
  • => row1=[1 2] and row2=[3 4]
  • => 행렬식 detA(n,n) = sum(j=1~n)[ (-1)**(1+j) * a[1][j] * detA(1,j) ]
  • Output: -2
• Input: [“5”,”0”,”<>”,”0”,”5”]
  • Output: 25
• Input: [“1”,”2”,”4”,”<>”,”2”,”1”,”1”,”<>”,”4”,”1”,”1”]
  • Output: -4

def MatrixDeterminant(strArr):
  # input
  mat, tmp = [], []
  for i, x in enumerate(strArr):
    if x == '<>':
      mat.append( tmp )
      tmp = []
    else:
      tmp.append( int(x) )
  # last one more
  mat.append( tmp )

  N, M = len(mat), len(tmp)
  # print(mat)

  # check square matrix
  if not all([len(r)==M for r in mat]) or N != M:
    return -1

  def calc_determinant(mat):
    if len(mat) < 2:
      return 0
    if len(mat) == 2:
      return mat[0][0]*mat[1][1] - mat[0][1]*mat[1][0]
    # divide and conquer
    determinant = 0
    for i in range(len(mat)):
      sub_mat = det_mat(mat,i)
      value = mat[0][i] * calc_determinant( sub_mat )
      determinant += (-1)**i * value
    return determinant

  # return detA matrix
  def det_mat(mat, i):
    if i >= len(mat): return []
    # slice matrix
    sub_mat = []
    for j in range(1, len(mat)):
      sub_mat.append([
        mat[j][k] for k in range(len(mat)) if k != i
        ])
    return sub_mat

  result = calc_determinant(mat)
  return result

# keep this function call here
print(MatrixDeterminant(input()))

다른 사람의 코드

numpy 를 알면 쉽게 푼다. np.linalg.det(matrix)

import numpy as np

def MatrixDeterminant(strArr):
  # input
  matrix = []
  row = []
  for char in strArr:
    if( char != "<>"):
      row.append(int(char))
    else:
      matrix.append(row)
      row = []
  matrix.append(row)

  # check N x N matrix
  if(len(matrix) != len(matrix[0])):
    return -1

  # calc Determinant
  return round(np.linalg.det(matrix))

# keep this function call here
print(MatrixDeterminant(input()))

참고: 역행렬 구하기

역행렬은 선형대수학에서 연립방정식을 풀기 위해 사용한다.

• 행렬 M = [ [1,2,3], [0,1,4], [5,6,0] ]
• 행렬식 det(M) = 1*(0-24) -2*(0-20) +3*(0-5)
• 전치행렬 Mt = [ [1,0,5], [2,1,6], [5,6,0] ]
  • 행과 열이 뒤바뀜: mat[i][j] => mat[j][i]
• 전치행렬 Mt 에 대한 소행렬의 행렬식 구하기
• 여인수 행렬 구하기: Adj(M)
• 역행렬 구하기 : 1/det(M) * Adj(M)

 

 

 

문제 76

Hamiltonian Path

해밀턴 경로를 만족하는지 판단하시오 (모든 꼭지점을 한번씩 지나는 경로)

• Input: [“(A,B,C,D)”,”(A-B,A-D,B-D,A-C)”,”(C,A,D,B)”]
  • node 집합: “(A,B,C,D)”
  • edge 집합: “(A-B,A-D,B-D,A-C)”
  • 해밀턴 경로: “(C,A,D,B)”
  • Output: “yes”
  • 만일 해밀턴 경로가 “(D,A,B,C)” 이면, 멈추는 정점 B를 출력
• Input: [“(A,B,C)”,”(B-A,C-B)”,”(C,B,A)”]
  • Output: yes
• Input: [“(X,Y,Z,Q)”,”(X-Y,Y-Q,Y-Z)”,”(Z,Y,Q,X)”]
  • Output: Q

다른 사람의 코드 (시간 없어서)

def HamiltonianPath(strArr):
  graph = build_graph(strArr[0], strArr[1])
  path = list(strArr[-1][1:-1].replace(',', ''))

  # 해밀턴 경로를 따라갈 수 있는지 검사
  for i in range( len(path) - 1 ):
    # 못따라 가면 멈추는 정점 반환
    if path[i+1] not in graph[path[i]]:
      return path[i]
  # 이상 없으면 yes
  return 'yes'


def build_graph(nodes, edges):
  nodes = list(nodes[1:-1].replace(',', ''))
  edges = edges[1:-1].split(',')

  graph = {}
  for node in nodes:
    graph[node] = []
  for edge in edges:
    a, b = edge[0], edge[2]
    graph[a].append(b)
    graph[b].append(a)
  return graph


print(HamiltonianPath(input()))

문제 77

LCS

LCS(longest common subsequence)의 길이를 구하시오

• 참고: [Longest Consecutive 문제] (/_posts/python-coding-test5.md#문제-44)
• Input: [“abcabb”,”bacb”]
  • Output: CS(“bab”, “acb”, “bcb”) 들의 최대 길이는 3
• Input: [“abc”,”cb”]
  • Output: 1
• Input: [“bcacb”,”aacabb”]
  • Output: 3

내가 제출한 코드

컴비네이션 이용

import itertools

def LCS(strArr):
  N = min([ len(x) for x in strArr ])
  # 최대 길이부터 탐색 (N ~ 1)
  for i in range(N,0,-1):
    combo1 = set( itertools.combinations( strArr[0], i ))
    combo2 = set( itertools.combinations( strArr[1], i ))
    if combo1 & combo2:
      return i
  return 0

# keep this function call here
print(LCS(input()))

다른 사람의 코드

재귀함수로 포지션(p1,p2) 이동하며 탐색

def LCS(strArr):

    def _LCS(p1, p2):
        # 종료 조건
        if p2 == len(s2) or p1 == len(s1):
            return 0
        # p1, p2 에서 일치하면 다음 재귀탐색 수행
        if s1[p1] == s2[p2]:
            return 1 + _LCS(p1+1, p2+1)
        # 일치하지 않으면, p1 또는 p2 를 한칸 이동하여 재귀탐색 수행
        # ==> 2가지 경우로 분기한 후, 제일 큰 수만 반환
        return max(_LCS(p1, p2+1), _LCS(p1+1, p2))

    s1, s2 = strArr
    return _LCS(0, 0)

# keep this function call here
print(LCS(input()))

set 연산자 복습

a = { 1,2,3 }
b = { 4,2,6 }

print( a | b, a | b == a.union(b) )
print( a & b, a & b == a.intersection(b) )
print( a - b, a - b == a.difference(b) )
print( a ^ b, a ^ b == a.symmetric_difference(b) )
"""
{1, 2, 3, 4, 6} True
{2} True
{1, 3} True
{1, 3, 4, 6} True
"""

문제 78

Pascals Triangle

파스칼의 삼각형에서 임의의 행에 대한 부분 배열이 주어질 때 다음값 구하기

• Input: [1,3,3] => Output: 1 ([1,3,3,1])
• Input: [1,5,10] => Output: 10 ([1,5,10,10,5,1])

내가 제출한 코드

def PascalsTriangle(arr):

  MAX_DEPTH = 20

  # 이것도 점화식이다. 이전 상태의 값을 재사용
  # F(n,m) = F(n-1,m-1) + F(n-1,m)

  # row = [1]
  row = [1,1]
  for i in range(2, MAX_DEPTH+1):
    next_row = [1]
    for j in range(1,len(row)):
        next_row.append( row[j-1]+row[j] )
    next_row.append(1)
    row = next_row
    # print(i, row)

    # stop if match row to arr
    if len(row) >= len(arr):
      if row[:len(arr)] == arr:
        break

  # code goes here
  return row[len(arr)] if len(row) > len(arr) else -1

# keep this function call here
print(PascalsTriangle(input()))
"""
2 [1, 2, 1]
3 [1, 3, 3, 1]
4 [1, 4, 6, 4, 1]
5 [1, 5, 10, 10, 5, 1]
"""

파스칼의 삼각형 특성

파스칼의 삼각형 만드는 법

• 왼쪽, 오른쪽 사선을 모두 ‘1’로 채우고
• 아래 원소의 값은 위쪽 행에 인접된 두 원소의 합

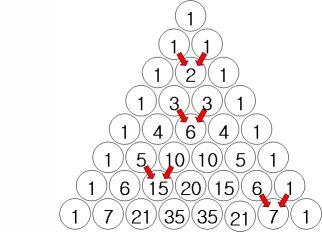
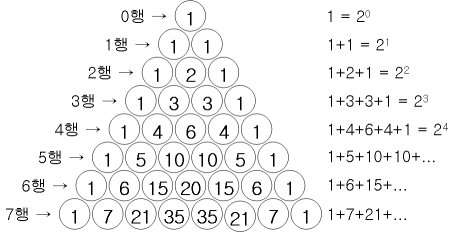
각 행의 합은 2의 거듭제곱과 같다.

문제 79

Approaching Fibonacci

가장 가까운 Fibonacci 수 찾기 (max_bound 로)

def ApproachingFibonacci(arr):
  MAX_NUM = 30

  def fibonacci(num):
    if num == 0:
      return 0
    if num == 1:
      return 1
    return fibonacci(num-1) + fibonacci(num-2)

  goal = sum(arr)
  for i in range(2, MAX_NUM):
    value = fibonacci(i)
    # check stop
    if value >= goal:
      break

  print(f'fib({i})={value} <= {goal}')
  return value - goal

# keep this function call here
print(ApproachingFibonacci(input()))

문제 80

Sudoku Quadrant Checker

9x9 매트릭스에서 행별로, 열별로 동일한 숫자가 반복되는지 체크 (legal 또는 해당 3x3의 번호)

• Input: 아래 텍스트 예제1
  • Output: 1,3,4
• Input: 아래 텍스트 예제2
  • Output: 3,4,5,9

예제 1)
["(1,2,3,4,5,6,7,8,1)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(1,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"]

예제 2)
["(1,2,3,4,5,6,7,8,9)"
,"(x,x,x,x,x,x,x,x,x)"
,"(6,x,5,x,3,x,x,4,x)"
,"(2,x,1,1,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,x)"
,"(x,x,x,x,x,x,x,x,9)"]

내가 작성한 코드

3x3 별로 쪼개서 중복된 숫자가 있는지 체크하면 될 줄 알았는데
문제를 잘못 이해했다. (수도쿠가 뭔지 몰라서)
각 행별로 체크하고, 각 열별로 체크해야 한다. (모두 2x9번)

• 입력데이터를 이중배열 mat 에 잘 적재하고 (x는 0변환)
  • (값, 보드id)
• 각 행별로 적재
  • 중복 숫자를 가진 보드id 저장
• 각 열별로 적재
  • 중복 숫자를 가진 보드id 저장
• 보드id 합쳐서 출력

def SudokuQuadrantChecker(strArr):
  # input
  mat = []
  for i in range(len(strArr)):
    arr = eval(strArr[i].replace('x','0'))
    n = i//3
    row = []
    for j in range(len(arr)):
      m = j//3
      board_id = str(n*3 + m + 1)
      row.append( (arr[j], board_id) )
    mat.append( row )

  # find boards with having dup_num
  def check_dup(arr):
    nums = {}
    for k,v in arr:
      if k == 0: continue
      boards = nums.setdefault(k,[])
      boards.append(v)
    dup_boards = {
      bid
      for boards in nums.values() if len(boards) > 1
      for bid in boards
      }
    # if dup_boards: print(dup_boards)
    return dup_boards

  boards = set()
  # check about all rows
  for arr in mat:
    boards |= check_dup(arr)
  # check about all cols
  for col in range(len(mat)):
    arr = []
    for row in mat:
      arr.append( row[col] )
    boards |= check_dup(arr)

  # output
  return ','.join(sorted(boards)) if boards else 'legal'

# keep this function call here
print(SudokuQuadrantChecker(input()))

 
 

끝!   읽어주셔서 감사합니다.